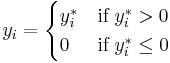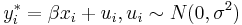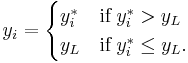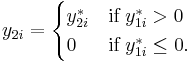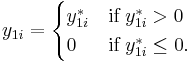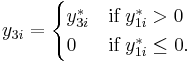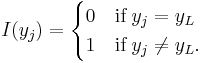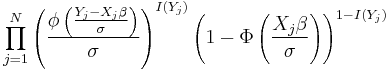Tobit model
| Economics |
|
Economies by region
|
| General categories |
|---|
|
History of economic thought Methodology · Mainstream & heterodox |
| Technical methods |
|
Game theory · Optimization Computational · Econometrics Experimental · National accounting |
| Fields and subfields |
|
Behavioral · Cultural · Evolutionary |
| Lists |
|
Journals · Publications |
| Business and Economics Portal |
The Tobit model is a statistical model proposed by James Tobin (1958) to describe the relationship between a non-negative dependent variable 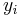 and an independent variable (or vector)
and an independent variable (or vector)  .
.
The model supposes that there is a latent (i.e. unobservable) variable 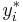 . This variable linearly depends on
. This variable linearly depends on  via a parameter (vector)
via a parameter (vector)  which determines the relationship between the independent variable (or vector)
which determines the relationship between the independent variable (or vector)  and the latent variable
and the latent variable 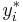 (just as in a linear model). In addition, there is a normally distributed error term
(just as in a linear model). In addition, there is a normally distributed error term 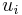 to capture random influences on this relationship. The observable variable
to capture random influences on this relationship. The observable variable 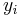 is defined to be equal to the latent variable whenever the latent variable is above zero and zero otherwise.
is defined to be equal to the latent variable whenever the latent variable is above zero and zero otherwise.
where 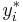 is a latent variable:
is a latent variable:
Contents |
Consistency
If the relationship parameter  is estimated by regressing the observed
is estimated by regressing the observed 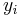 on
on  , the resulting ordinary least squares regression estimator is inconsistent. It will yield a downwards-biased estimate of the slope coefficient and an upwards-biased estimate of the intercept. Takeshi Amemiya (1973) has proven that the maximum likelihood estimator suggested by Tobin for this model is consistent.
, the resulting ordinary least squares regression estimator is inconsistent. It will yield a downwards-biased estimate of the slope coefficient and an upwards-biased estimate of the intercept. Takeshi Amemiya (1973) has proven that the maximum likelihood estimator suggested by Tobin for this model is consistent.
Interpretation
The  coefficient should not be interpreted as the effect of
coefficient should not be interpreted as the effect of  on
on 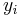 , as one would with a linear regression model; this is a common error. Instead, it should be interpreted as the combination of (1) the change in
, as one would with a linear regression model; this is a common error. Instead, it should be interpreted as the combination of (1) the change in 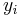 of those above the limit, weighted by the probability of being above the limit; and (2) the change in the probability of being above the limit, weighted by the expected value of
of those above the limit, weighted by the probability of being above the limit; and (2) the change in the probability of being above the limit, weighted by the expected value of 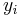 if above.[1]
if above.[1]
Variations of the Tobit model
Variations of the Tobit model can be produced by changing where and when censoring occurs. Amemiya (1985) classifies these variations into five categories (Tobit type I - Tobit type V), where Tobit type I stands for the first model described above. Schnedler (2005) provides a general formula to obtain consistent likelihood estimators for these and other variations of the Tobit model.
Type I
The Tobit model is a special case of a censored regression model, because the latent variable 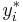 cannot always be observed while the independent variable
cannot always be observed while the independent variable  is observable. A common variation of the Tobit model is censoring at a value
is observable. A common variation of the Tobit model is censoring at a value 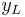 different from zero:
different from zero:
Another example is censoring of values above 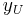 .
.
Yet another model results when 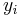 is censored from above and below at the same time.
is censored from above and below at the same time.
The rest of the models will be presented as being bounded from below at 0, though this can be generalized as we have done for Type I.
Type II
Type II Tobit models introduce a second latent variable.
Heckman (1987) falls into the Type II Tobit. In Type I Tobit, the latent variable absorb both the process of participation and 'outcome' of interest. Type II Tobit allows the process of participation/selection and the process of 'outcome' to be independent, conditional on x.
Type III
Type III introduces a second observed dependent variable.
The Heckman model falls into this type.
Type IV
Type IV introduces a third observed dependent variable and a third latent variable.
Type V
Similar to Type II, in Type V we only observe the sign of 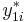 .
.
The likelihood function
Below are the likelihood and log likelihood functions for a type I Tobit. This is a Tobit that is censored from below at 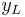 when the latent variable
when the latent variable 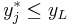 . In writing out the likelihood function, we first define an indicator function
. In writing out the likelihood function, we first define an indicator function 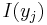 where:
where:
Next, we mean 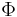 to be the standard normal cumulative distribution function and
to be the standard normal cumulative distribution function and  to be the standard normal probability density function. For a data set with N observations the likelihood function for a type I Tobit is
to be the standard normal probability density function. For a data set with N observations the likelihood function for a type I Tobit is
Etymology
The term “tobit” was derived from Tobin's name and by adding the suffix "-it," as for the 1964 probit model by Arthur Goldberger.[2]
See also
References
- ^ McDonald, John F.; Moffit, Robert A. (1980), "The Uses of Tobit Analysis", The Review of Economics and Statistics (The MIT Press) 62 (2): 318–321, http://www.jstor.org/stable/1924766
- ^ International Encyclopedia of the Social Sciences (2008)
Further reading
- Amemiya, Takeshi (1973), "Regression analysis when the dependent variable is truncated normal", Econometrica (The Econometric Society) 41 (6): 997–1016, doi:10.2307/1914031, http://www.jstor.org/stable/1914031
- Amemiya, Takeshi (1984), "Tobit models: A survey", Journal of Econometrics 24 (1–2): 3–61, doi:10.1016/0304-4076(84)90074-5
- Amemiya, Takeshi (1985), Advanced Econometrics, Oxford: Basil Blackwell, ISBN 0631133453
- Schnedler, Wendelin (2005), "Likelihood estimation for censored random vectors", Econometric Reviews 24 (2): 195–217, doi:10.1081/ETC-200067925
- Tobin, James (1958), "Estimation of relationships for limited dependent variables", Econometrica (The Econometric Society) 26 (1): 24–36, doi:10.2307/1907382, http://www.jstor.org/stable/1907382